Here is the
control flow block diagram of our algorithm:

The control flow of our algorithm
Let's take
a step - by - step look at our algorithm:
5. 1. Edge detection
We used
Matlab's built in function for edge detection and chose the Canny
algorithm. Choosing the right low and high thresholds was not an easy
task. For now these are hard - coded so that they give the optimal
results for the view points of our data and for the lighting of the
scenes. In a more sophisiticated implementation they could be
determined automatically.
5. 2. Detecting the table boundaries and geometry.
The key
algorithm behind our project was the Hough transform.
We
implemented two different versions of the algorithm. One for fitting
lines on the scene and one for fitting circles.
But how
does Hough transform work?
5. 2. 1 Hough transform in a nutshell.
The
main idea behind this brilliant algorithm is a transformation of
image features, namely edges, to a space where it is more obvious
where straight lines are formed, as well as other parametric curves,
depending on the programmer's choice. The following image shows the
Hough transform for lines.
For
each pixel on an edge, the transform computes its distance from the
center of the image and the angle that the position vector forms. If
we then plot all these (distance, angle) pairs we get the right
image. All the points on the same line form curves that pass through
the same point.
Now it
is obvious which points belong to the same line in the original
image.

Hough transform for straight lines
5. 2. 2 Computing bounding boxes, geometry and
perspective.
5. 2. 2. 1 Bounding box.
In order to compute the bounding box of the
pool table we ran our Hough lines algorithm on the edges of the
scene. This revealed all the straight lines. First we computed the
line with the minimum distance from the center of the table and
erased the lines with the same slope as this one. By doing this we
were able to recursively compute the 4 lines that form the
bounding box of the table.
5. 2. 2. 2
Geometry.
The
four corners of the table were computed by looking at all possible
intersections of the 4 bounding lines and then determining the one
with the 4th smallest distance from the centroid (the mean in both
directions) of those intersections. We by throwing away the points
with distances bigger than this we were left with the 4 corners of
the table.
5. 2. 2. 3 Inverse perspective matrix
computation.
We have measured the dimensions of our table
so that we know the true coordinates of our table. By
combining the estimated corners on the image plane with the
true ones we were able to compute the inverse perspective
transformation matrix.

The inverse perspective mapping.
What we did was to try to find a 3 X 3 matrix that would
map each point on the image plane onto the world (or table)
plane.
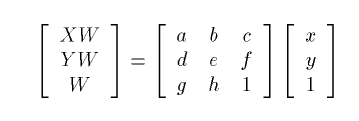
The
most difficult task here was to make sure that both the image
plane and the table plane had the same center. In order to
make sure that this is the case we translated the table
plane and then when the mapping was done we translated
back.
5. 3. Detecting the balls.
Having detected the table corners we ran our implementation of
Hough transform for circles on the region of interest defined by the
bounding box.
For each ball a triplet was computed, namely the center
coordinates  and the
radius
and the
radius  .
.
We used Hough transform again parametrized for
circles.

Hough transform for circles.
Hough transform in general is a voting algorithm. In the case
of circles for each pixel on an edge and for each radius in a given
range of interest a circle is drawn. The pixels where most circles go
through accumulate more votes and come up as maxima in the accumulator
array. For a specific sensitivity of the algorithm one can apply a
threshold to the accumulator and discover the first n strongest
center pixels.
For our case here is a 3D surf plot of one of our accumulators.

5. 4. Table bird's
eye view.
Constructing the table as seen from above was an easy
task once the inverse perspective transform matrix was available. We
took the centers of the balls in homogenous coordinates, mapped them
to the table plane and rehomogenized the transformed centers by
dividing by their 3rd component (w).
For the visualization of this part we used a trick. We
constructed two images. One depicting the table from above and one for
a ball. (The color of the ball is not relevant - we are only
interested in the geometry of the scene). Then for each of the
transformed centers we glued (by changing the pixels) the ball image
on the table image.

